Aufgabe B 2.1
Gegeben sind die Ebne E: 3x1+6x2+4x3=16 und eine Geradenschar durch
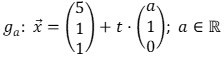 .
.
a) Bestimmen Sie den Schnittpunkt der Geraden g4 mit der Ebene E.
Welche Gerade der Schar ist orthogonal zu g4?
(3 VP)
b) Berechnen Sie den Schnittwinkel von g4 und E.Für welche Werte von a mit -10<a<10 hat der Schnittwinkel von ga und E die Weite 10°?
(3 VP)
c) Begründen Sie, dass alle Geraden ga in der Ebene F: x3=1 liegen.Es gibt eine Gerade h, die durch den Punkt P(5|1|1) geht und in F liegt, aber nicht zu der Schar gehört.
Bestimmen Sie eine Gleichung der Geraden h.
(3 VP)
Aufgabe B 2.2
Bei einem Biathlonwettbewerb läuft ein Athlet eine 2,5 km lange Runde, dann schießt er liegend fünf Mal; anschließend läuft er eine zweite Runde und schießt stehend fünf Mal; nach einer dritten Runde erreicht er das Ziel. Für jeden Fehlschuss muss er direkt nach dem Schießen eine 200 m lange Strafrunde laufen. Aufgrund der bisherigen Schießleistungen geht der Trainer davon aus, dass der Athlet stehend mit 88% und liegend mit 93% Wahrscheinlichkeit trifft. Es wird vereinfachend davon ausgegangen, dass die Ergebnisse der einzelnen Schüsse voneinander unabhängig sind.
a) Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Athlet stehend bei fünf Schüssen genau viermal trifft.
(1 VP)
b) Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Athlet im gesamten Wettbewerb höchstens einmal eine Strafrunde laufen muss.(3 VP)
c) Der Athlet möchte seine Leistungen im Stehendschießen verbessern und künftig mit über 95% Wahrscheinlichkeit bei fünf Schüssen mindestens vier Mal treffen.Welche Trefferwahrscheinlichkeit muss er dafür mindestens erreichen?
(2 VP)